『式の展開』の電卓
スポンサーリンク
入力例)(x+1)(x+5)
スポンサーリンク
このページを友達に教える
電卓の使い方
展開する式を電卓に入力し「展開」ボタンを押してください。
やり直す場合は「クリア」ボタンを押すと電卓に入力された式が削除されます。
分数の入力に対応しました。(2020.6.7追記)
式の展開の問題反復練習にはこちらの問題出題ツールをご利用ください。
式の展開の問題出題ツール
目次
スポンサーリンク
式の展開の解説
式のカッコをはずすことを「式を展開(てんかい)する」と言います。要するに展開とは式の変形になります。カッコを使った掛け算の形の式をカッコをはずして足し算や引き算の形に式を変形します。
(x+1)(x-6) = x2-5x-6
分配法則を使って展開する
展開の基本は、分配法則を使ってカッコをはずすことです。分配法則というのはカッコ内の項にそれぞれ数を掛ける手法です。

5(x-8) = 5x-40
3(2x+3) = 6x+9
-3(x+5) = -3x-15
x(x+5) = x2+5x
カッコ同士の分配法則
(x+1)(x+2)のようにカッコが隣り合っている場合にも分配法則を使ってカッコをはずします。このときに注意したいのは、同類項ができる場合がありますので同類項の計算まで忘れずにおこないましょう。
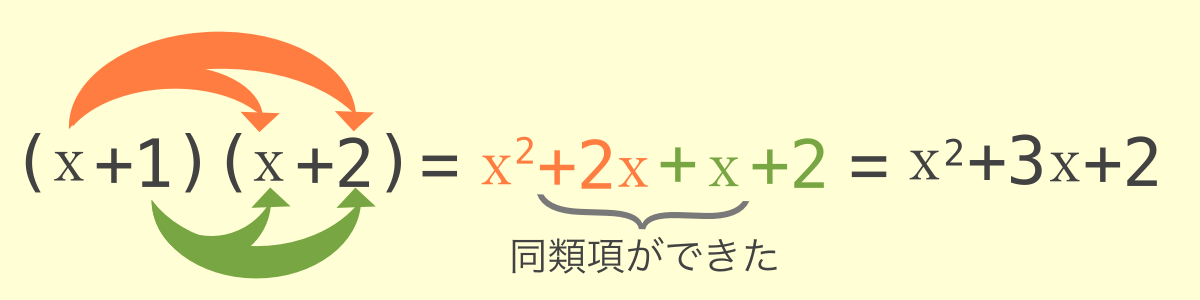
(x+2)(x+3)
= x2+3x+2x+6
= x2+5x+6
(x-2)(x+4)
= x2+4x-2x-8
= x2+2x-8
(x+3)(x-3)
= x2-3x+3x-9
= x2-9
カッコ内の項が3つ以上ある場合
もしカッコ内の項が3つ以上あるような場合でも同じように分配法則を使ってそれぞれに掛け算をおこないます。
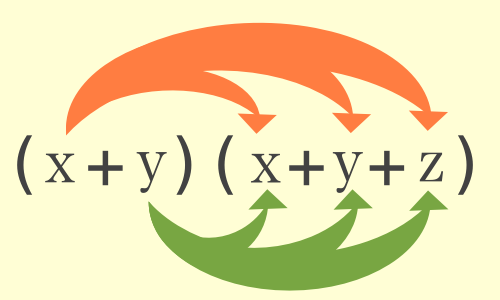
(x+2)(x+y+3)
= x2+xy+3x+2x+2y+6
= x2+xy+5x+2y+6
カッコ2乗の展開
(x+2)2のようにカッコに2乗がついている場合には、(x+2)(x+2)に置き換えて分配法則をおこないます。
(x+3)2
= (x+3)(x+3)
= x2+3x+3x+9
= x2+6x+9
分数を含んだ展開
分数を含んだ式の展開も基本的には整数の式の展開と同じ要領で解くことができます。
ただ、分数を含んだ展開を解く場合に気をつけなければいけない点は、同類項の計算です。分数と分数や分数と整数を計算する場合に同類項として計算できるのは、分母と分子がどちらも同類項の場合のみです。また約分が可能になることもあるので約分することも忘れずにおこないましょう。
スポンサーリンク
式の展開の問題例
= x2+2xy-5x-6y+6
= x2-4x-4x+16
= x2-8x+16
= x-15
= x2-3x+15
関連ページ
よく見られているページ
- 約分の電卓
- 分母と分子を入力すると約分された分数を表示する電卓です。大きい数の分数でも簡単に約分をおこなうことができます。
- 分数の混合計算の電卓
- 分数の四則演算ができる電卓です。3つ以上の分数の計算をおこなったり整数や帯分数との計算にも対応しています。
- 因数分解の電卓
- 入力された式を因数分解できる電卓です。解き方がいくつもある因数分解ですが、この電卓を使えば簡単に因数分解がおこなえます。
- 連立方程式の電卓
- 2つの方程式を入力することで連立方程式として解くことができる電卓です。計算方法は加減法または代入法で選択でき、途中式も表示されます。
- 中学数学の問題出題ツール一覧
- 中学数学の問題をプログラムで作成して出題するツールです。問題を何度でも解く練習ができて答えもすぐに確認することができます。
- 因数分解の問題出題ツール
- 因数分解の問題を出題するツールです。条件を指定することで因数分解の問題が出題され、反復練習に役に立つツールです。
中学数学の無料問題集
