『通分』の電卓
スポンサーリンク
スポンサーリンク
このページを友達に教える
電卓の使い方
通分をおこなう2つの分数の分母・分子を入力して「計算」ボタンを押してください。
分母や分子が少数になっている分数の通分にも対応しています。
3つ以上の分数で通分をおこないたい場合は「分数追加」ボタンを押してください。
通分をやり直す場合は「クリア」ボタンを押すと入力された数値が削除されます。
約分ができる電卓はこちらのページをご利用ください。
約分の電卓
目次
スポンサーリンク
通分の解説
2つの分数の分母を同じにすることを通分(つうぶん)と言います。どうして分母を同じにする通分が必要になるかと言うと、分数同士の大小比較や計算(足し算や引き算)をするために通分がおこなわれます。
言葉だけだとイメージしにくいと思いますので、図を使って通分を説明します。以下の図は2分の1と3分の1を図にしたものです。
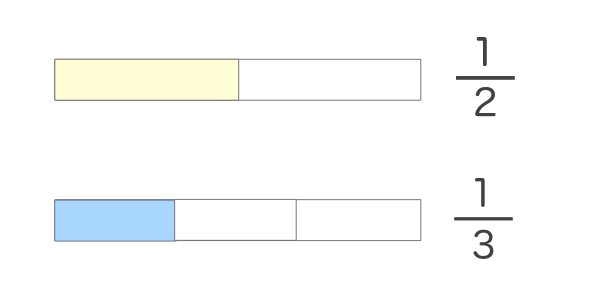
とがそれぞれの分数の分子である1を表していますが、同じ1でも長さが違うことがわかるかと思います。これは分母がそれぞれの分数で違うために同じ1でも条件が違うためです。
それでは上の図をそれぞれ6等分してみます。
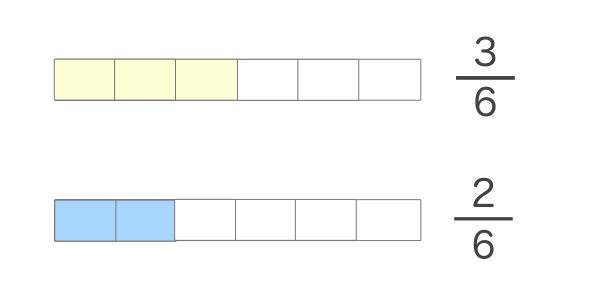
6等分してみると2分の1は6分の3に、3分の1は6分の2になりました。そして1個分のとが同じ長さになっていることがわかるかと思います。つまり分母を同じにすることで分子の条件が同じになったということになります。
条件が同じになれば以下の図のように足し算をおこなうこともできます。
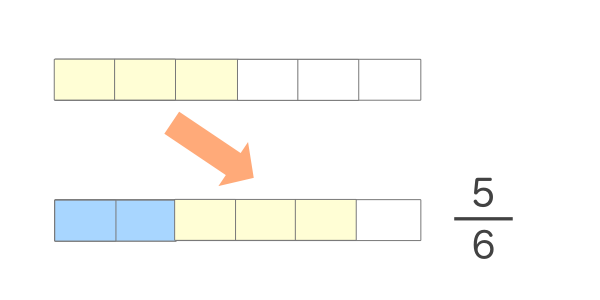
このように分母が違う分数を同じ分母にして条件を合わせることによって計算をおこなったり大きさの比較をできるようにすることが通分をおこなう意味になります。
通分をおこなう方法
通分の方法は、まずそれぞれの分母の最小公倍数を求めます。この最小公倍数がそれぞれの分母となります。最小公倍数を元の分母で割った数を分子に掛けます。
分母の3と4の最小公倍数は12
▼分母を12にするために4を掛ける
▼分母を12にするために3を掛ける
▼通分した分数
※最小公倍数とは
対象の数を整数で掛けた数の事を倍数(ばいすう)と言います。2つの数のそれぞれの倍数で共通した倍数のうち最小の倍数の事を最小公倍数(さいしょうこうばいすう)と言います。
【例】3と5の最小公倍数
3の倍数 → 3,6,9,12,15,18,21,.....
5の倍数 → 5,10,15,20,25,.....
3と5で共通する倍数のうち最小の数は15なので最小公倍数は「15」
3つ以上の分数の通分
3つ以上の分数を通分する場合も、2つの分数の通分と同様に分母を合わせることでおこなえます。それぞれの分数の分母の最小公倍数を求め、その最小公倍数が分母になるように掛け算をおこないます。
分母の2と3と4の最小公倍数は12
▼分母を12にするために6を掛ける
▼分母を12にするために4を掛ける
▼分母を12にするために3を掛ける
▼通分した分数
少数を含んだ分数の通分
分母や分子が少数になっている分数を通分することもあります。そのまま通分できないこともないですが、最小公倍数を求めるのが面倒になったりするので一工夫を加えます。
少数が含まれている分数を通分する場合には、まず少数の分数を整数の分数になおします。例えば0.2/0.4のような分数は分母・分子に10をそれぞれ掛けて2/4という整数の分数にします。このままでも通分はできますが約分が可能な場合は約分までやっておくと通分の分数が小さくできます。2/4は1/2に約分することができます。あとは通常の通分と同じように分母の最小公倍数を求めて分母を同じにします。
▼少数の分数を整数にし約分
分母の2と3の最小公倍数は6
▼分母を6にするために3を掛ける
▼分母を6にするために2を掛ける
▼通分した分数
スポンサーリンク
通分の問題例
分母の3と8の最小公倍数は24
左:分母を24にするため8倍にする
右:分母を24にするため3倍にする
通分された分数
分母の9と6の最小公倍数は18
左:分母を18にするため2倍にする
右:分母を18にするため3倍にする
通分された分数
関連ページ
よく見られているページ
- 約分の電卓
- 分母と分子を入力すると約分された分数を表示する電卓です。大きい数の分数でも簡単に約分をおこなうことができます。
- 分数の混合計算の電卓
- 分数の四則演算ができる電卓です。3つ以上の分数の計算をおこなったり整数や帯分数との計算にも対応しています。
- 因数分解の電卓
- 入力された式を因数分解できる電卓です。解き方がいくつもある因数分解ですが、この電卓を使えば簡単に因数分解がおこなえます。
- 連立方程式の電卓
- 2つの方程式を入力することで連立方程式として解くことができる電卓です。計算方法は加減法または代入法で選択でき、途中式も表示されます。
- 中学数学の問題出題ツール一覧
- 中学数学の問題をプログラムで作成して出題するツールです。問題を何度でも解く練習ができて答えもすぐに確認することができます。
- 因数分解の問題出題ツール
- 因数分解の問題を出題するツールです。条件を指定することで因数分解の問題が出題され、反復練習に役に立つツールです。
中学数学の無料問題集
