『分数の足し算』の電卓
スポンサーリンク
帯分数を使う
スポンサーリンク
このページを友達に教える
電卓の使い方
足し算をおこなう2つの分数の分母・分子を電卓に入力して「計算」ボタンを押してください。
少数を含んだ分数の足し算にも対応しています。少数の分数の場合、整数の分数に変換して計算がおこなわれます。
帯分数の足し算にも対応しています。「帯分数を使う」にチェックすると帯分数の整数分が入力できるようになります。帯分数の分数を入力しなければ整数としての計算も可能です。
計算をやり直す場合は「クリア」ボタンを押すと電卓に入力された数値が削除されます。
3つ以上の分数計算や四則混合計算はこちらの電卓ページをご利用ください。
分数の混合計算
目次
- 分数の足し算の解説
- 分母が同じ分数の足し算
- 分母が違う分数の足し算
- 整数と分数の足し算
- 帯分数と分数の足し算
- 少数が含まれる分数の足し算
- 3つ以上の分数の足し算
- 分数の足し算まとめ
- 分数の足し算の問題例
- 関連ページ
スポンサーリンク
分数の足し算の解説
分数の足し算をおこなう場合、分母が違うと単純に数を足すことはできません。以下の図を見てください。
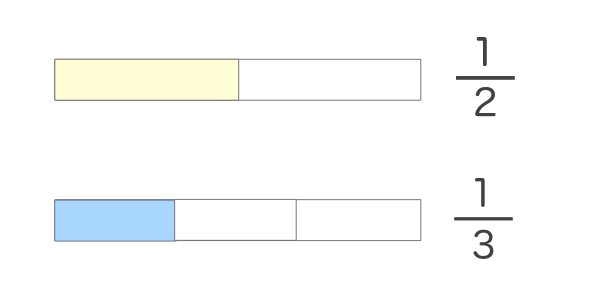
上の図は1/2と1/3を図にしたもので、とが分子の1を表しています。このように分子が同じ1でも大きさは違っていることがわかります。なので1+1=2のような事はできないのです。
では、どうすればいいかと言うと、分子の1を同じ大きさに合わせてあげる必要があります。1/2と1/3の図をそれぞれ6等分にしてみます。
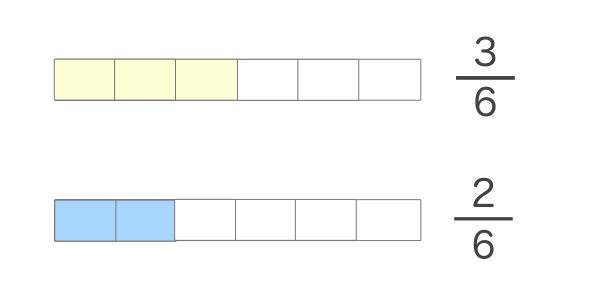
6等分することによって、1/2は3/6、1/3は2/6となりました。そして分子1個分の大きさが同じになったことがわかるかと思います。こうする事で足し算をおこなうことも可能になります。
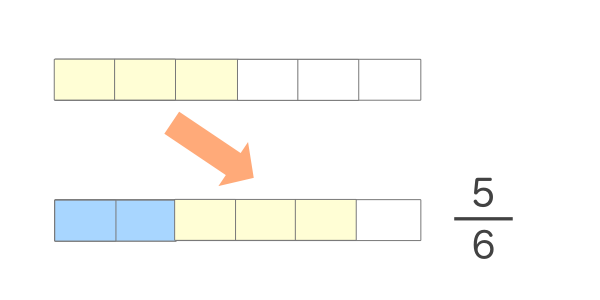
これが分数の足し算をおこなう場合の考え方になります。それぞれの分数の分母を同じにすることで分子1個分の大きさを合わせて足し算がおこなえるようにします。この分母を合わせることを通分(つうぶん)と言います。
ここまでで分数の足し算の考え方を解説しましたが、実際に分数を足し算する場合の具体例をあげていきます。
分母が同じ分数の足し算
分母が同じ分数を足し算する場合は通分をおこなう必要はありません。分母を共通にし分子同士を足し算します。分母も足さないように注意してください。足すのはあくまでも分子のみです。
▼足し算
分母が違う分数の足し算
分母が違う分数の足し算をおこなう場合は、まず通分をおこないます。通分というのは分母が違う分数同士を同じ分母に合わせてあげることです。
通分の手順は、まず分母の最小公倍数を求めます。そしてそれぞれの分母に何を掛ければその最小公倍数になるかを求め、その数を分母と分子にも掛けます。
分母の2と3の最小公倍数は6
分母の2を最小公倍数の6にするには3を掛けばいいので、分母と分子に3を掛ける
分母の3を最小公倍数の6にするには2を掛けばいいので、分母と分子に2を掛ける
通分が完了
通分したら分母が同じ分数の足し算と同じように分母を共通にし分子同士を足し算します。分母は足さないようにしてください。足し算はあくまで分子のみです。
また注意する事として足し算をおこなった分数が約分できることがあります。約分ができる場合にはしっかり約分までおこないましょう。約分ができていないと不正解になることもあります。
約分の電卓
▼通分
▼足し算
※約分ができる場合は約分をおこなう
※約分とは
分数の分母と分子を同じ数で割りきれなくなるまで割ることを約分と言います。
整数と分数の足し算
整数と分数で足し算をおこなう場合は、まず整数を分数にします。整数を分数にするには、分母を1に、分子を整数の数にします。あとは分数同士の足し算と同じように分母が異なるときは通分をおこない、分子の足し算をします。
▼整数を分数にする
▼通分
▼足し算
帯分数と分数の足し算
帯分数と分数で足し算をおこなう場合は、まず帯分数を分数にします。帯分数を分数にするには、帯分数の整数と分母を掛けて分子を足すと分数に変えることができます。あとは分数同士の足し算と同じように通分して足し算をおこないます。この手順は帯分数同士で計算するときも同じ手順になります。
▼帯分数を分数にする
▼通分
▼足し算
少数が含まれる分数の足し算
少し意地悪な問題だと、少数が含まれる分数の足し算が出ることもあります。分数の分母や分子が少数になっているということです。こういった場合にはまず少数を整数にしてあげましょう。
分母と分子に同じ数を掛けた(もしくは割った)分数は同値分数となります。これで少数が含まれた分数が整数の分数に直すことができます。あとは通常の足し算のように通分して分子を足し算します。
▼少数を整数にする
▼通分して足し算
少数が含まれる分数を整数の分数になおすときに注意したいのは、必ず分母と分子に同じ数を掛けることです。桁が違う場合に違う数を掛けてしまうこともあるかもしれませんので注意してください。
3つ以上の分数の足し算
これまでで2つの分数の足し算はわかったと思いますが、分母が異なる分数が3つ以上あるときの足し算はどうするのでしょうか?このような場合でも基本的な考え方は同じです。すべての分数を通分して分子を足し算します。
▼通分
▼足し算
ただ上記の方法では足し算をする分数が多くなるほど通分が難しくなってしまいます。4つ、5つと分数が増えていけば、分母の最小公倍数を見つけるだけでも大変です。そういった場合に別の方法として、最初の分数にひとつずつ分数を足していく方法もあります。この方法でも答えは同じになりますので、通分が難しいというような問題のときはこちらの分数の足し算を使うといいかと思います。
▼先頭の2つの分数を通分して足し算
▼3番目の分数を通分して足し算
分数の足し算まとめ
分数の足し算の基本は
1.分母を合わせる(通分)
2.分子同士を足す
3.約分できるなら約分
この3つのステップでおこないます。
分数の計算は初めは難しいと感じるかもしれません。その原因はおそらく分母を合わせるための通分です。通分はいろんな数を考えないといけないので混乱しがちです。これを克服するには問題の反復練習が必要です。慣れてくれば小さい数ならスッと通分できるようになるのでここは努力が必要になります。
それと何度も言ってますが最後の約分は忘れないようにしましょう。せっかく通分して計算をしても最後の約分ができていなければ台無しになってしまいます。最後まで気を抜かずに約分できるかを分数の計算では忘れないようにしましょう。
スポンサーリンク
分数の足し算の問題例
関連ページ
よく見られているページ
- 約分の電卓
- 分母と分子を入力すると約分された分数を表示する電卓です。大きい数の分数でも簡単に約分をおこなうことができます。
- 分数の混合計算の電卓
- 分数の四則演算ができる電卓です。3つ以上の分数の計算をおこなったり整数や帯分数との計算にも対応しています。
- 因数分解の電卓
- 入力された式を因数分解できる電卓です。解き方がいくつもある因数分解ですが、この電卓を使えば簡単に因数分解がおこなえます。
- 連立方程式の電卓
- 2つの方程式を入力することで連立方程式として解くことができる電卓です。計算方法は加減法または代入法で選択でき、途中式も表示されます。
- 中学数学の問題出題ツール一覧
- 中学数学の問題をプログラムで作成して出題するツールです。問題を何度でも解く練習ができて答えもすぐに確認することができます。
- 因数分解の問題出題ツール
- 因数分解の問題を出題するツールです。条件を指定することで因数分解の問題が出題され、反復練習に役に立つツールです。
中学数学の無料問題集
