『約分』の電卓
スポンサーリンク
スポンサーリンク
このページを友達に教える
電卓の使い方
約分をおこなう分数の分母・分子を電卓に入力して「計算」ボタンを押してください。
この電卓は小数の約分にも対応しています。小数の分数の場合は、整数にして約分されます。
約分をやり直す場合は「クリア」ボタンを押すと電卓に入力された数値が削除されます。
通分ができる電卓はこちらのページをご利用ください。
通分の電卓
目次
スポンサーリンク
約分の解説
分母と分子が異なっている2つの分数であっても、分母と分子が同じ数を掛けた分数(もしくは同じ数を割った分数)であれば等しい分数となります。
分数をイメージにしてみるとわかりやすいかと思います。下の図を見てみると分母と分子が違う分数でも同じ意味だということがわかりやすいのではないでしょうか?
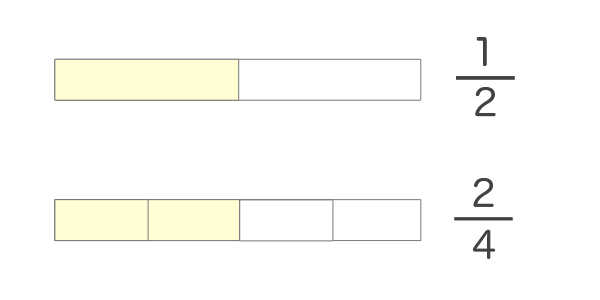
また分数を小数に変換してみても同じ意味の分数ということがわかります。分数は分子を分母で割ることで小数に変えることができます。
この分数の性質を利用して、分母・分子を同じ数で割って、分母と分子を最小の分数にすることを約分(やくぶん)と言います。
約分の方法
約分をおこなう方法としては、まず基本的な方法として分母・分子を同じ数で割っていき割り切れなくなるまで繰り返すという方法があります。
この方法は割り算ができればできる約分の方法です。ただ分母・分子の数が大きいと割る回数も多くなって計算が大変になることもあります。
約分をおこなうもうひとつの方法として、分母と分子の最大公約数を求めて、その最大公約数で分母・分子を割ると1度で約分をすることができます。
16と32の最大公約数は16
※最大公約数とは
対象の数を整数で割って余りがでない数の事を約数(やくすう)と言います。2つの数のそれぞれの約数で共通した約数のうち最大の約数の事を最大公約数(さいだいこうやくすう)と言います。
【例】24と16の最大公約数
24の約数 → 1,2,3,4,6,8,12,24
16の約数 → 1,2,4,8,16
24と16で共通する約数のうち最大の数は8なので最大公約数は「8」
分母と分子の最大公約数を求めることができれば簡単に約分をおこなえます。
分母が1になったら整数にする
約分すると分母が1になることもあります。分母が1の場合は整数と同じになりますので整数にしましょう。
16と4の最大公約数は4
分母や分子が小数の場合の約分
分母や分子が小数の場合は、整数になおして約分をおこないます。例えば0.3なら10を掛ける、0.03なら100を掛けるというように整数になるように掛け算をおこないます。注意点としては分母と分子に同じ数を掛けるということです。分母だけに掛けたり分子だけに掛けたりすると違う意味の分数になってしまいますので必ず分母・分子に同じ数を掛けてください。
小数を整数にする場合には、必ず分母・分子に同じ数を掛けることに注意してください。例えば、分母が整数で分子が小数のような分数の場合には、分子だけに掛けるのではなく、分母にも同じ数を掛ける必要があります。
帯分数の約分
帯分数を約分する場合は、帯分数の整数部分はそのままにして分数部分だけを約分します。
帯分数を分数にして約分してみるとわかりますが、結局分数部分だけを約分したのと答えは同じになるので分数部分だけを約分したほうが計算が簡単にできます。
どうして約分が必要なのか?
同じ意味の分数ならどうして約分が必要なのかを思うかもしれません。約分をおこなう目的は主に2つあります。
1.数の計算をおこなう際に分母と分子の数が大きいと計算が面倒になるため約分をおこなって分母と分子を最小にして計算をおこないやすくする。
2.答えが分数の場合に約分してわかりやすい分数にする。
1については約分を習ったときにはほとんど気にする必要がないですが、計算が複雑になっていくと計算の途中で約分を活用することもでてきます。2については約分できる分数は約分までするということがルールになっていたりもします。テストで約分までおこなわないと間違いとされることもあるため約分できる場合は必ず約分をおこなうクセをつけておくといいと思います。
スポンサーリンク
約分の問題例
関連ページ
よく見られているページ
- 約分の電卓
- 分母と分子を入力すると約分された分数を表示する電卓です。大きい数の分数でも簡単に約分をおこなうことができます。
- 分数の混合計算の電卓
- 分数の四則演算ができる電卓です。3つ以上の分数の計算をおこなったり整数や帯分数との計算にも対応しています。
- 因数分解の電卓
- 入力された式を因数分解できる電卓です。解き方がいくつもある因数分解ですが、この電卓を使えば簡単に因数分解がおこなえます。
- 連立方程式の電卓
- 2つの方程式を入力することで連立方程式として解くことができる電卓です。計算方法は加減法または代入法で選択でき、途中式も表示されます。
- 中学数学の問題出題ツール一覧
- 中学数学の問題をプログラムで作成して出題するツールです。問題を何度でも解く練習ができて答えもすぐに確認することができます。
- 因数分解の問題出題ツール
- 因数分解の問題を出題するツールです。条件を指定することで因数分解の問題が出題され、反復練習に役に立つツールです。
中学数学の無料問題集
