『因数分解』の電卓
スポンサーリンク
入力例)x2+4x+3
スポンサーリンク
このページを友達に教える
電卓の使い方
因数分解を行う式を電卓に入力し「因数分解」ボタンを押してください。
置き換えや公式を連続して使うなどの複雑な因数分解では途中式も表示されますので解き方の手順がわかります。
この電卓は中学で習う因数分解に対応しています。3次式などの高校レベルの因数分解には当電卓では対応していません。
やり直す場合は「クリア」ボタンを押すと電卓に入力された式が削除されます。
因数分解の反復練習にはこちらの問題出題ツールをご利用ください。
因数分解の問題出題ツール
目次
- 因数分解の解説
- 基本:共通因数をまとめる
- 基本:公式1でまとめる
- 基本:公式2でまとめる
- 基本:公式3でまとめる
- 基本:たすきがけ
- 応用:共通因数でくくって公式に当てはめる
- 応用:カッコを置き換える
- 応用:連続して因数分解
- 応用:項を分けて因数分解
- 因数分解の問題例
- 関連ページ
スポンサーリンク
因数分解の解説
因数分解とは、多項式を積の形に変形することです。こう聞くとわかりにくいかもしれませんが、要するにカッコ()でくくった掛け算の形に変形するという事です。計算をして答えを求めるものではなく、式を別の形に変えることが因数分解です。
x2+6x+5 = (x+1)(x+5)
カッコで囲われた式のカッコをはずすのが式の展開ですが、因数分解はこの逆でカッコでくくるように式の変形をおこないます。
この特性を活かせば因数分解をおこなった式が合っているかを確認する場合には、因数分解した式を展開してみて元の式に戻れば因数分解できていると判断することができます。
基本:共通因数をまとめる
因数分解でまず基本となるのは、共通因数をまとめるということです。
式の項を数字の因数や文字に分解して、それぞれの項で共通するもののことを共通因数と言います。言葉だけではわかりずらいと思いますので、共通因数でまとめる因数分解の例をあげて解説します。
xy+8y
xyを分解すると、xとy
8yを分解すると、8とy
yが共通しているので、yをまとめることができる
= y(x+8)
もし文字が2乗となっているような場合には、その文字が2つに分解できると考えます。
x2+4x
x2を分解すると、xとx
4xを分解すると、4とx
xが共通しているので、xをまとめることができる
= x(x+4)
文字は比較的簡単に分解できるますが、数字は因数で分解して共通の因数を探す必要があります。上記の例では数字の因数は1と自身の数だけになるため無視していますが、以下の例では数字を因数に分解して共通因数を探して因数分解をおこないます。
5x2-15x
5x2を分解すると、1と5とxとx
15xを分解すると、1と3と5と15とx
5とxが共通しているので、5とxをまとめることができる
= 5x(x-3)
この共通因数でくくるのが因数分解の基本となります。数字だけや文字だけをまとめると間違いになるため、両方でまとめることができる場合には必ず両方でまとめるようにしてください。
基本:公式1でまとめる
公式1
ポイントになるのはaとbです。2つ目の項はaとbの和、3つ目の項はaとbの積になっています。つまりaとbの組み合わせを見つけることが公式1を使った因数分解でのポイントとなります。
x2+6x+5
6xは、(1+5)x
5は、(1×5)
1と5が公式のaとbになるため
= (x+1)(x+5)
この公式1を使った因数分解では、符号に注意する必要があります。符号によって3つのパターンがあります。
▼(a+b)xと(a×b)の項が正のとき
x2+(a+b)x+ab = (x+a)(x+b)
▼(a×b)の項が負のとき
x2+(a+b)x-ab = (x-a)(x+b)
▼(a+b)xの項が負で(a×b)の項が正のとき
x2-(a+b)x+ab = (x-a)(x-b)
x2+5x+6
= (x+2)(x+3)
x2+x-6
= (x-2)(x+3)
x2-5x+6
= (x-2)(x-3)
基本:公式2でまとめる
公式2
公式2では、2番目の項が3番目の項の平方根×2になることがポイントです。この公式2は公式1と似ていて、公式1の場合は異なる数字の和と積だったのに対して、公式2は同じ数字の和と積になっています。
x2+6x+9
9は32であり、3×2は6なので公式2に当てはまる
= (x+3)2
公式2を使う因数分解でも符号によって2つのパターンがあります。
▼2axの項が正のとき
x2+2ax+a2 = (x+a)2
▼2axの項が負のとき
x2-2ax+a2 = (x-a)2
x2+8x+16
= (x+4)2
x2-8x+16
= (x-4)2
ちなみに公式2を使う因数分解では、a2の項がマイナスになることはありません。同じ数字同士の2乗なので必ずプラスになります。なのでa2の項がマイナスの場合はこの公式2に当てはまることはありません。
基本:公式3でまとめる
公式3
2乗のものを2乗のもので引いた式は、和と差の積に変換できるのが因数分解の公式3です。文字の2乗はわかりやすいですが、気をつけたいのは数字の2乗です。数字は平方根が整数になるかを確認する必要があります。
x2-16
16は42なので公式3に当てはまる
= (x+4)(x-4)
公式3を使う因数分解では、他の公式と違い符号によるパターンはありませんが、項が逆になっているときには注意しましょう。
-9+x2
項を入れ替えると、x2-9となり
9は32なので公式3に当てはまる
= (x+3)(x-3)
基本:たすきがけ
たすきがけと呼ばれる手法を使った因数分解をおこないます。以下の問題を例に解説します。
まず、以下のような図を作り、問題の係数を配置します。
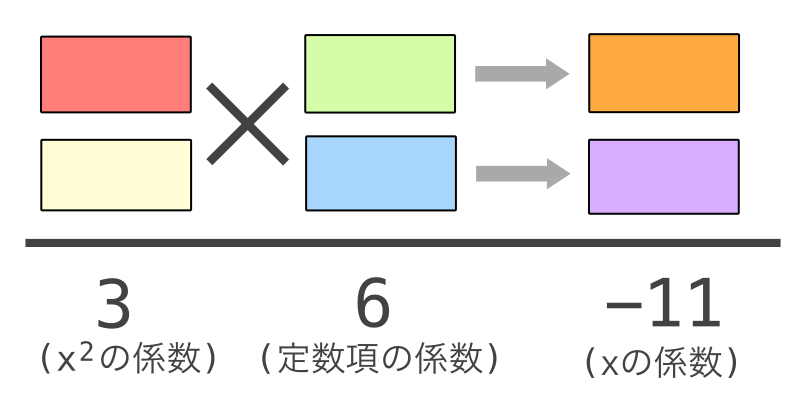
図のとには、積がx2の係数である3となる数字が入ります。3になる積は3×1や1×3があります。
同じようにとには、積が定数項の係数である6となる数字が入ります。6になる積は1×6、2×3、3×2、6×1、-1×-6、-2×-3、-3×-2、-6×-1があります。マイナスの数字もあるという点に注意してください。
数字を実際に入れてみてななめがけ、つまり×をに、×をに入れます。そして、とを足した値がxの係数である-11になるパターンを探します。
数字を入れて図が成り立つパターンを探すと以下のように数字が入ります。
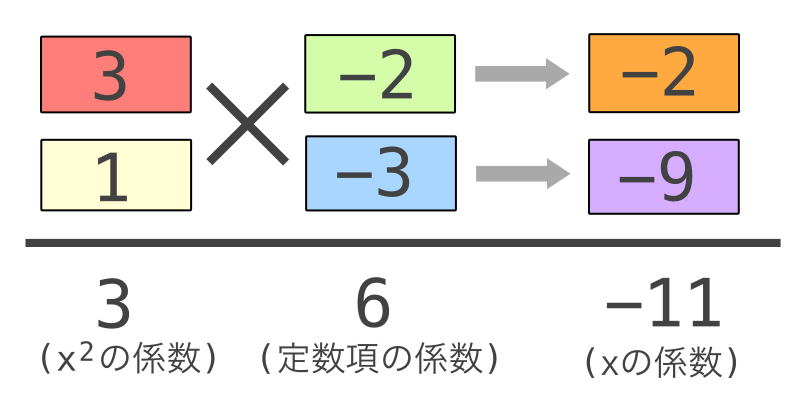
図ができたら以下のように答えを導くことができます。ななめがけするのはこの答えの配置に持って行きやすいようにです。
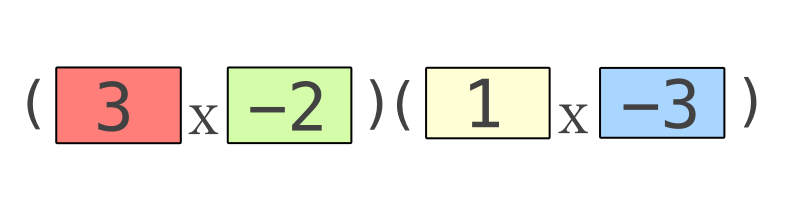
つまり、答えは(3x-2)(x-3)となります。
応用:共通因数でくくって公式に当てはめる
ここからは基本をふまえて応用編になります。共通因数でくくると公式に当てはめるという2つの因数分解の基本を組み合わせます。まず式を共通因数でくくった後、カッコ内の式を公式に当てはめるという因数分解の方法です。
4x2y+28xy+48y
▼4yでくくる
= 4y(x2+7x+12)
▼カッコ内を公式1に当てはめる
= 4y(x+3)(x+4)
ax2-10ax+25a
▼aでくくる
= a(x2-10x+25)
▼カッコ内を公式2に当てはめる
= a(x-5)2
3x3-48x
▼3xでくくる
= 3x(x2-16)
▼カッコ内を公式3に当てはめる
= 3x(x+4)(x-4)
応用:カッコを置き換える
カッコがある式では、カッコを文字に置き換えて因数分解を試みます。カッコ内が同じときは同じ文字に置き換えてから共通因数をくくったり公式に当てはめます。最後に置き換えたカッコを元に戻すことを忘れずにおこないましょう。
x(a+b)-7(a+b)
▼(a+b)をAに置き換える
= xA-7A
▼Aでくくる
= A(x-7)
▼置き換えたAを元に戻す
= (a+b)(x-7)
(a+b)2-7(a+b)+10
▼(a+b)をAに置き換える
= A2-7A+10
▼公式1に当てはめる
= (A-2)(A-5)
▼置き換えたAを元に戻す
= (a+b-2)(a+b-5)
応用:連続して因数分解
式を部分的に因数分解してカッコでくくった部分を文字に置き換えてさらに因数分解をおこないます。
x2+10x+25-36a2
▼部分的に公式2に当てはめる
= (x+5)2-36a2
▼カッコをAに置き換える
= A2-36a2
▼公式3に当てはめる
= (A+6a)(A-6a)
▼置き換えたAを元に戻す
= (x+5+6a)(x+5-6a)
a2-x2+6x-9
▼部分的に-1でくくって公式2に当てはめる
= a2-(x2-6x+9)
= a2-(x-3)2
▼カッコをAに置き換える
= a2-A2
▼公式3に当てはめる
= (a+A)(a-A)
▼置き換えたAを元に戻す
= (a+x-3)(a-x+3)
※Aの前がマイナスの場合、符号を反転させる
応用:項を分けて因数分解
式の項を分割してそれぞれの共通因数をくくった後に、カッコを置き換えしさらに共通因数をくくります。
xa-xb-5a+5b
▼式を分割
= (xa-xb)-(5a-5b)
※後ろのカッコの前はマイナスなので、カッコ内の符号は反転させる
▼カッコ内の共通因数をくくる
= x(a-b)-5(a-b)
▼(a-b)をAに置き換える
= xA-5A
▼Aをくくる
= A(x-5)
▼置き換えたAを元に戻す
= (a-b)(x-5)
スポンサーリンク
因数分解の問題例
= 4x(x+4)
= (y-9)(y+2)
= (a-12)2
= (b+9)(b-9)
= 4y(x2-9)
▼カッコ内を公式3に当てはめる
= 4y(x+3)(x-3)
= x2-2xA+A2
▼公式2に当てはめる
= (x-A)2
▼置き換えたAを元に戻す
= (x-a+b)2
※Aの前がマイナスなので符号を反転
= 9a2-(x-10)2
▼カッコをAに置き換える
= 9a2-A2
▼公式3に当てはめる
= (3a+A)(3a-A)
▼置き換えたAを元に戻す
= (3a+x-10)(3a-x+10)
※Aの前がマイナスの場合は符号を反転
= (x3-2x2)-(3xy-6y)
▼カッコ内を共通因数でくくる
= x2(x-2)-3y(x-2)
▼カッコ内をAに置き換える
= x2A-3yA
▼Aでくくる
= A(x2-3y)
▼置き換えたAを元に戻す
= (x-2)(x2-3y)
関連ページ
よく見られているページ
- 約分の電卓
- 分母と分子を入力すると約分された分数を表示する電卓です。大きい数の分数でも簡単に約分をおこなうことができます。
- 分数の混合計算の電卓
- 分数の四則演算ができる電卓です。3つ以上の分数の計算をおこなったり整数や帯分数との計算にも対応しています。
- 因数分解の電卓
- 入力された式を因数分解できる電卓です。解き方がいくつもある因数分解ですが、この電卓を使えば簡単に因数分解がおこなえます。
- 連立方程式の電卓
- 2つの方程式を入力することで連立方程式として解くことができる電卓です。計算方法は加減法または代入法で選択でき、途中式も表示されます。
- 中学数学の問題出題ツール一覧
- 中学数学の問題をプログラムで作成して出題するツールです。問題を何度でも解く練習ができて答えもすぐに確認することができます。
- 因数分解の問題出題ツール
- 因数分解の問題を出題するツールです。条件を指定することで因数分解の問題が出題され、反復練習に役に立つツールです。
中学数学の無料問題集
