『二乗に比例する関数』の電卓
スポンサーリンク
このページを友達に教える
電卓の使い方
値の代入
二乗に比例する関数の式と代入する値を電卓に入力し「計算」ボタンを押してください。
xの値を代入するとy、yの値を代入するとxが算出されます。
比例定数
点のxとyの値を入力して「計算」ボタンを押してください。
変域
二乗に比例する関数の式とxの変域を電卓に入力し「計算」ボタンを押してください。
変化の割合
xの変化値と二乗に比例する関数の式もしくはyの変化値を電卓に入力し「計算」ボタンを押してください。
目次
スポンサーリンク
二乗に比例する関数の解説
yを比例定数×x2の式で表せる関数のことを二乗に比例する関数と言います。例えば、y=2x2のような式が二乗に比例する関数です。
二乗に比例する関数は以下のような基本式になります。
二乗に比例する関数の基本式
この基本式のうち、aは比例定数(ひれいていすう)と言います。xとyは変数(へんすう)と言い、xの値が変わればyの値も変わっていくものです。
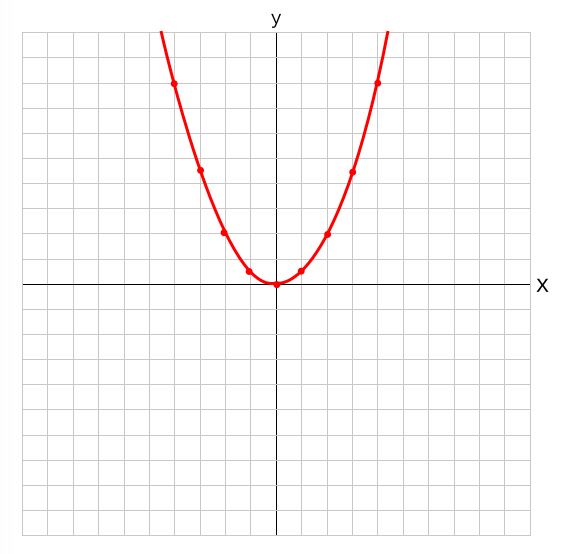
二乗に比例する関数のグラフには以下のような特徴があります。
・y軸に対して対称な放物線になる
・必ず原点を通る
・比例定数が正のときは上に開き、負のときは下に開く
二乗に比例する関数のグラフを書く場合にはxの値を式に代入してyの値を求め、点を結ぶように放物線を書きます。
値の代入
二乗に比例する関数の式とxに値がわかっている場合、式に値を代入することでyの値を求めることができます。
y=3×2×2
y=12
同様にyの値からxの値を求めることもできます。ただしxの値は絶対値が同じで正と負の2つの値が算出されます。これはグラフにするとわかりやすいと思いますが二乗に比例する関数のグラフはy軸に対して対称な放物線となるため、同じyの値となる点は2つあるためです。
16=4x2
x2=4
x=±2
比例定数を求める
1つの点のxとyの値がわかっていれば、基本式に値を代入することで比例定数を求めることができます。
8=a×22
8=4a
a=2
変域を求める
変域とはグラフの範囲のことで、横の範囲がxの変域、縦の範囲がyの変域となります。
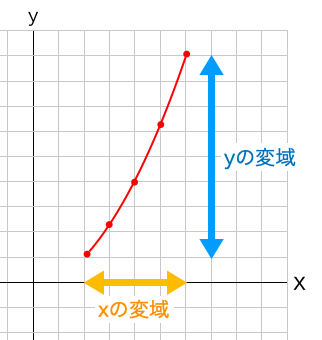
二乗に比例する関数の場合、グラフが放物線となるため、xの変域がy軸をまたぐ場合には、yの最小値は0になることに注意する必要があります。
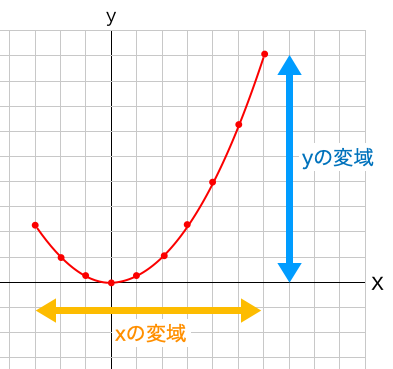
y=2x2について、xの変域が2≦x≦5のときのyの変域を求めなさい。
8≦y≦50
y=3x2について、xの変域が-2≦x≦3のときのyの変域を求めなさい。
0≦y≦27
y=-3x2について、xの変域が-1≦x≦4のときのyの変域を求めなさい。
-48≦y≦0
変化の割合を求める
二乗に比例する関数の変化の割合は以下の式で求めることができます。
この式は一次関数と同じものですが、一次関数の変化の割合は一定なのに対して、二乗に比例する関数の変化の割合は一定にはなりません。
式とxの増加量がわかる場合には、式にxの値を代入しyの増加量を求めてから変化の割合を算出します。
x=-1のとき、y=3
x=3のとき、y=27
スポンサーリンク
二乗に比例する関数の問題例
y=48
y=-8
x2=4
x=±2
9a=27
a=3
4a=-8
a=-2
x=1のとき、y=-2
関連ページ
よく見られているページ
- 約分の電卓
- 分母と分子を入力すると約分された分数を表示する電卓です。大きい数の分数でも簡単に約分をおこなうことができます。
- 分数の混合計算の電卓
- 分数の四則演算ができる電卓です。3つ以上の分数の計算をおこなったり整数や帯分数との計算にも対応しています。
- 因数分解の電卓
- 入力された式を因数分解できる電卓です。解き方がいくつもある因数分解ですが、この電卓を使えば簡単に因数分解がおこなえます。
- 連立方程式の電卓
- 2つの方程式を入力することで連立方程式として解くことができる電卓です。計算方法は加減法または代入法で選択でき、途中式も表示されます。
- 中学数学の問題出題ツール一覧
- 中学数学の問題をプログラムで作成して出題するツールです。問題を何度でも解く練習ができて答えもすぐに確認することができます。
- 因数分解の問題出題ツール
- 因数分解の問題を出題するツールです。条件を指定することで因数分解の問題が出題され、反復練習に役に立つツールです。
中学数学の無料問題集
