『一次関数』の電卓
スポンサーリンク
このページを友達に教える
電卓の使い方
値の代入
一次関数の式と代入する値を電卓に入力し「計算」ボタンを押してください。
xの値を代入するとy、yの値を代入するとxが算出されます。
式を出す
傾き(切片)・点1・点2のうち、2項目を入力して「計算」ボタンを押してください。
3項目とも入力された場合、点2が無視されます。
目次
スポンサーリンク
一次関数の解説
yをxの一次式で表せる関数のことを一次関数と言います。例えば、y=3x+1のような式が一次関数です。y=2x2+3のような二次式になっている関数は二次関数になります。
一次関数には以下のような基本式があります。
一次関数の基本式
この基本式のうち、aとbは定数(ていすう)と言い値が変わりません。またxとyは変数(へんすう)と言い、xの値が変わればyの値も変わっていくものです。
一次関数はグラフを使って表すことができます。例えばy=2x+1という一次関数は以下のようなグラフになります。
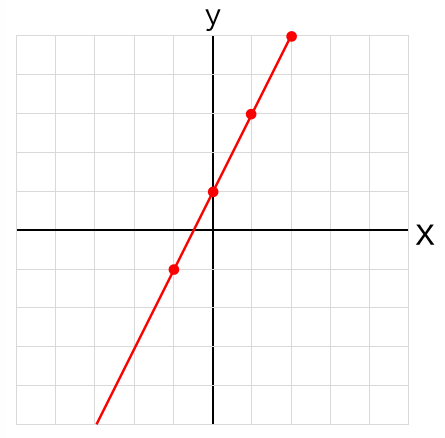
どうしてこのようなグラフになるかと言うと、一次関数の式に値を代入することで値の変化をグラフにすることができます。例えばxの値が0の場合、一次関数の式に代入するとy=2×0+1となり、y=1というようにyの値を求めることができます。このように片方の値を代入すればもう片方の値も算出することができ、その点を結べばグラフになるということです。
ちなみに一次関数のグラフはかならず直線になります。
グラフの傾き(変化の割合)
一次関数の基本式y=ax+bのaはグラフの傾きを表しています。変化の割合とも言われます。例えば、y=2x+1の傾きの値は2となります。
傾きの値は、2点の座標からも求めることができます。2点の座標から傾きを求める場合には以下の式で求めます。
傾き(変化の割合)の求め方
▼点(1,3)と点(2,7)の傾き(変化の割合)は?
グラフの切片
一次関数の基本式y=ax+bのbはグラフの切片(せっぺん)を表しています。切片とは、xが0の場合のyの値を指します。例えば以下のグラフの切片は1となります。

傾きと1点から式を出す
傾きと1点の座標がわかれば一次関数の式を出すことができます。傾きと点の座標を一次関数の基本式に入れ、切片を求めて式にします。
点(2,4)を通り、傾きが3の一次関数の式を出しなさい。
▼y=ax+bにa=3,x=2,y=4を代入
4=3×2+b
-b=6-4
-b=2
b=-2
▼基本式にaとbの値を代入して式を出す
y=3x-2
切片と1点から式を出す
切片と1点の座標がわかれば一次関数の式を出すことができます。切片と点の座標を一次関数の基本式に入れ、傾きを求めて式にします。
点(2,8)を通り、切片が-2の一次関数の式を出しなさい。
▼y=ax+bにb=-2,x=2,y=8を代入
8=2a-2
-2a=-2-8
-2a=-10
a=5
▼基本式にaとbの値を代入して式を出す
y=5x-2
2点から式を出す
2点の座標から一次関数の式を出す場合には、まず2点の増加量から傾きを算出します。傾きがわかったら基本式に傾きと点の座標を代入して切片を求めます。
点(2,5)と点(4,9)を通る一次関数の式を出しなさい。
▼2点から傾きを求める
▼y=ax+bにa=2,x=2,y=5を代入
5=2×2+b
-b=4-5
-b=-1
b=1
▼基本式にaとbの値を代入して式を出す
y=2x+1
スポンサーリンク
一次関数の問題例
y=8
2x=-4
x=-2
y=5
▼y=ax+bにa=3,x=3,y=7を代入
7=3×3+b
-b=9-7
-b=2
b=-2
▼基本式にaとbの値を代入して式を出す
y=3x-2
▼y=ax+bにb=-1,x=2,y=9を代入
9=2a-1
-2a=-1-9
-2a=-10
b=5
▼基本式にaとbの値を代入して式を出す
y=5x-1
▼傾きを求める
▼y=ax+bにa=-2,x=0,y=-2を代入
-2=-2×0+b
-b=2
b=-2
▼基本式にaとbの値を代入して式を出す
y=-2x-2
関連ページ
よく見られているページ
- 約分の電卓
- 分母と分子を入力すると約分された分数を表示する電卓です。大きい数の分数でも簡単に約分をおこなうことができます。
- 分数の混合計算の電卓
- 分数の四則演算ができる電卓です。3つ以上の分数の計算をおこなったり整数や帯分数との計算にも対応しています。
- 因数分解の電卓
- 入力された式を因数分解できる電卓です。解き方がいくつもある因数分解ですが、この電卓を使えば簡単に因数分解がおこなえます。
- 連立方程式の電卓
- 2つの方程式を入力することで連立方程式として解くことができる電卓です。計算方法は加減法または代入法で選択でき、途中式も表示されます。
- 中学数学の問題出題ツール一覧
- 中学数学の問題をプログラムで作成して出題するツールです。問題を何度でも解く練習ができて答えもすぐに確認することができます。
- 因数分解の問題出題ツール
- 因数分解の問題を出題するツールです。条件を指定することで因数分解の問題が出題され、反復練習に役に立つツールです。
中学数学の無料問題集
