『相似比』の電卓
スポンサーリンク
相似な図形の対応する辺
辺の長さを求める(省略可)
スポンサーリンク
このページを友達に教える
電卓の使い方
相似な図形の対応する辺の長さを入力すると、相似比が算出できます。
「辺の長さを求める」に入力すると相似比と辺の長さからわからない辺の長さを計算します。
計算をやり直す場合は「クリア」ボタンを押すと入力された数値が削除されます。
目次
スポンサーリンク
相似比の解説
ある図形を拡大もしくは縮小した図形のことを相似な図形と言います。
相似な図形には以下のような特徴があります。
・対応する辺の長さの比は全て等しい
・対応する角度はそれぞれ等しい
相似比
前述しているとおり、相似な図形には「対応する辺の長さの比が全て等しい」という特徴があります。
例えば、三角形ABCを2倍に拡大した三角形DEFがあるとします。
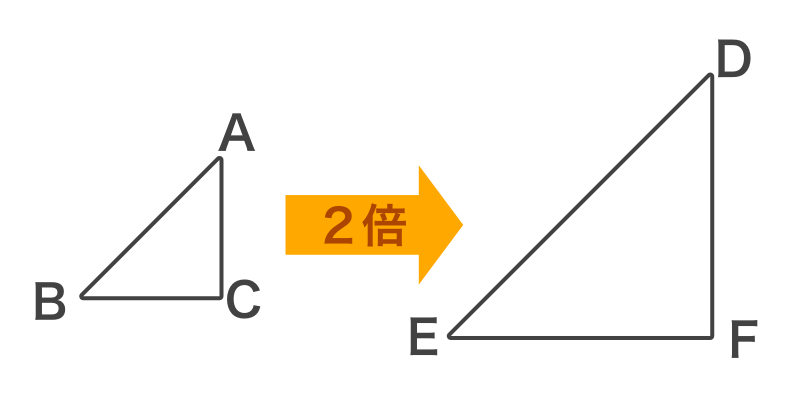
対応する辺はABとDE・BCとEF・ACとDFになりますが、これらの比はすべて1:2となります。このような相似な図形における辺の長さの比のことを相似比(そうじひ)と言います。
相似比を求める問題としては以下のような問題があります。
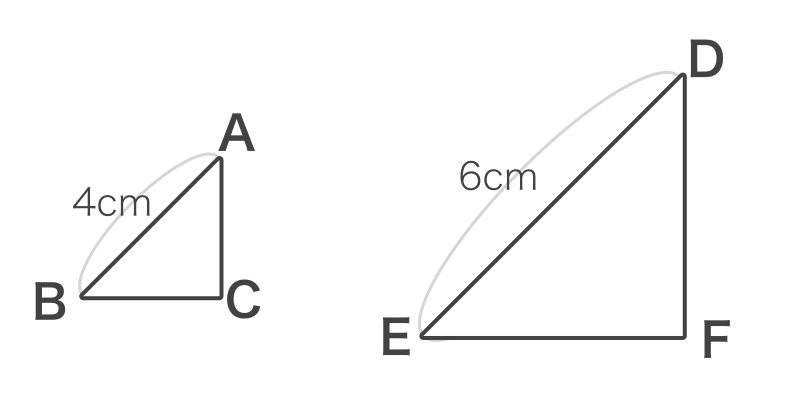
この問題では、対応するABとDEの長さがわかっているので比は4:6ですが、比はなるべく簡単にしておく必要がありますので、相似比としては2:3となります。
辺の長さを求める
相似な図形は対応する辺の長さの比が全て同じになります。この相似比の特徴を使って辺の長さを求める問題もよく出ます。
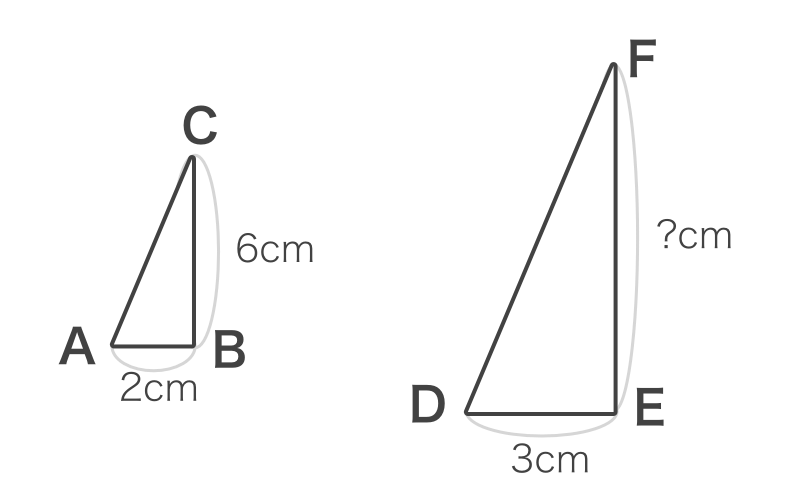
辺の長さを求める場合はまず相似比を求めます。長さがわかっていて対応しているABとDEから相似比は2:3だということがわかります。
相似比が2:3であれば、長さがわかっているBCと求めるEFも2:3であることがわかりますので、「2:3=6:EF」という比の式が成り立ちます。これを解けばEFの長さが9cmであることがわかります。
スポンサーリンク
相似比の問題例
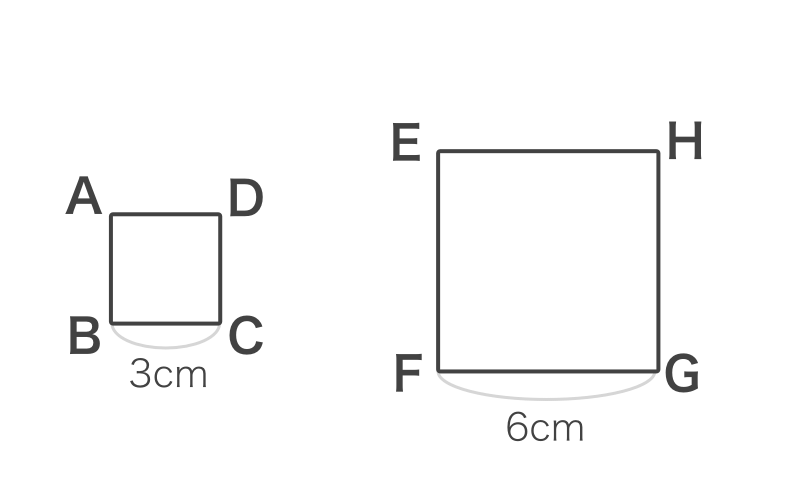
= 1:2
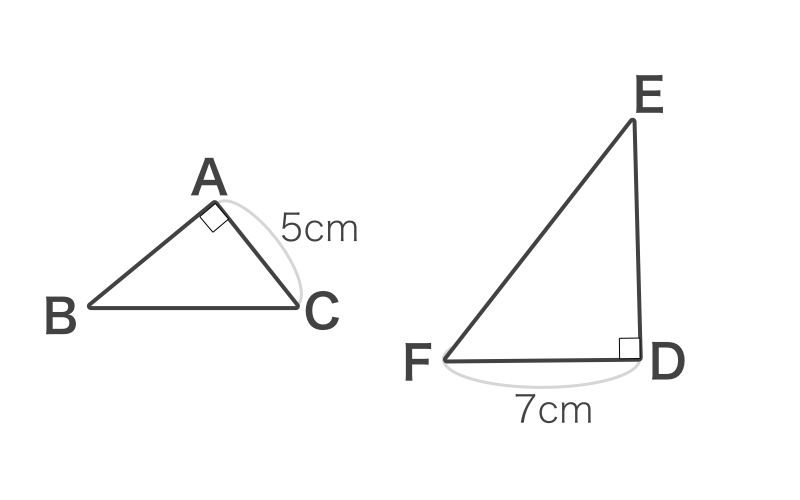
▼相似比
= 3:5
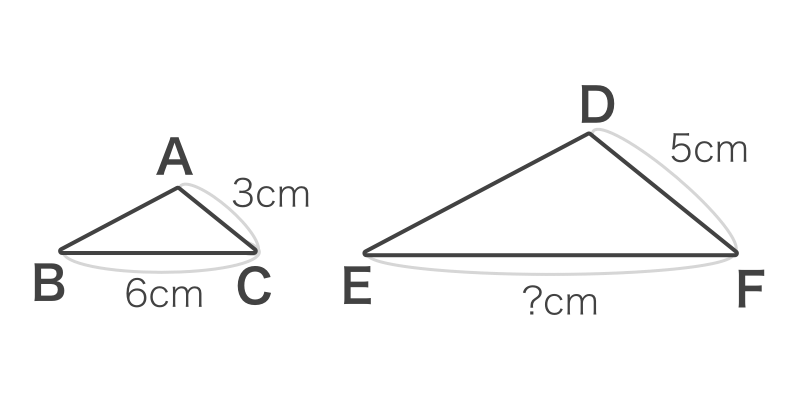
▼辺の長さを求める
3:5 = 6:x
3x = 30
x = 10cm
関連ページ
よく見られているページ
- 約分の電卓
- 分母と分子を入力すると約分された分数を表示する電卓です。大きい数の分数でも簡単に約分をおこなうことができます。
- 分数の混合計算の電卓
- 分数の四則演算ができる電卓です。3つ以上の分数の計算をおこなったり整数や帯分数との計算にも対応しています。
- 因数分解の電卓
- 入力された式を因数分解できる電卓です。解き方がいくつもある因数分解ですが、この電卓を使えば簡単に因数分解がおこなえます。
- 連立方程式の電卓
- 2つの方程式を入力することで連立方程式として解くことができる電卓です。計算方法は加減法または代入法で選択でき、途中式も表示されます。
- 中学数学の問題出題ツール一覧
- 中学数学の問題をプログラムで作成して出題するツールです。問題を何度でも解く練習ができて答えもすぐに確認することができます。
- 因数分解の問題出題ツール
- 因数分解の問題を出題するツールです。条件を指定することで因数分解の問題が出題され、反復練習に役に立つツールです。
中学数学の無料問題集
