『比の計算』の電卓
スポンサーリンク
※3箇所入力してください
スポンサーリンク
このページを友達に教える
電卓の使い方
求める箇所以外の比(3箇所)を入力して「計算」ボタンを押してください。
小数の比も計算できます。
計算をやり直す場合は「クリア」ボタンを押すと入力された数値が削除されます。
目次
スポンサーリンク
比の計算の解説
比は、その比に同じ数を掛けるか割った別の比と同じという性質を持っています。
3:6 = 1:2(左の比を3で割ったのが右の比)
比の関係は分数の関係によくにています。分数の場合も、分母と分子に同じ数を掛けるもしくは割った分数と同じです。約分したら同じ分数になるということですね。
比のわからない部分を求める
比が同じ数を掛けるか割った別の比と同じという性質を利用することで、比の一部がわからなくても計算で求めることができます。2つの比のうち、3箇所がわかっていれば残りの1箇所を計算して求めることができるというわけです。
→ それぞれの比の左側が3倍に増えているので、右側も3倍すれば□が求められる
→ □=2×3=6
→ それぞれの比の右側が1/4になっているので、左側も1/4すれば□が求められる
→ □=12÷4=3
中学生向けの比の計算方法としては、方程式のような解き方もできます。比のわからない部分をxとして、比の外側と内側を掛ける方法です。外側と内側を掛けて=で結んで方程式の要領で解いていけばxの値を求めることができます。
例えば、A:B=C:xという比を計算する場合は、外側のAとx、内側のBとCを掛けて=で結びます。するとA×x=B×Cとなり、方程式の要領で解くことができます。
1:2 = 3:x
▼比の外側と内側を掛ける
1×x = 2×3
x = 6
12:4 = x:1
▼比の外側と内側を掛ける
12×1 = 4×x
12 = 4x
x = 3
比の計算を図形に応用する
比の計算をよく使う場面として、図形に使うことがよくあります。
ある図形を拡大もしくは縮小した図形(相似な図形と言います)があり、対応する辺からわからない辺の長さを求めるときに辺の計算が用いられます。例えば、以下のような三角形を拡大した別の三角形があり、わからない辺の長さを求めます。
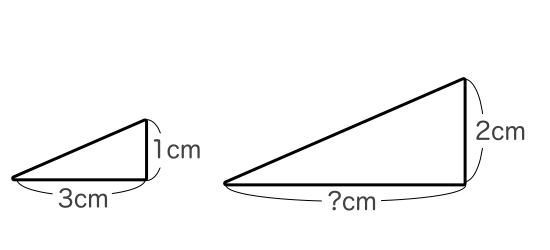
上記のような相似な図形から辺の長さを求める場合には、対応する辺を比として考えます。両方の図形で対応する辺がわかっているのは右の辺なのでこの辺を比にすると1cm:2cmとなります。そして、長さがわからないところがある辺の比は3cm:?cmになります。相似な図形では各辺の比は同じになるため、1cm:2cm=3cm:?cmという比が成り立ちます。前の比から後ろの比が3倍になっていることがわかるので、2cmを3倍して6cmがわからない辺の長さということになります。
注意点として、図形に比の計算が使えるのは、拡大または縮小した2つの図形の場合です。対応する角度が違うなど相似でない図形同士では比の計算は使うことができません。また面積や体積についての比の計算は別の方法がありますので詳しくはこちらをご参照ください。
相似の面積比・体積比
スポンサーリンク
比の計算の問題例
1:3 = 5:□
□ = 3×5 = 15
18:9 = 6:□
□ = 9÷3 = 3
2:□ = 8:12
□の4倍が12なので、12を4で割る
□ = 12÷4 = 3
関連ページ
よく見られているページ
- 約分の電卓
- 分母と分子を入力すると約分された分数を表示する電卓です。大きい数の分数でも簡単に約分をおこなうことができます。
- 分数の混合計算の電卓
- 分数の四則演算ができる電卓です。3つ以上の分数の計算をおこなったり整数や帯分数との計算にも対応しています。
- 因数分解の電卓
- 入力された式を因数分解できる電卓です。解き方がいくつもある因数分解ですが、この電卓を使えば簡単に因数分解がおこなえます。
- 連立方程式の電卓
- 2つの方程式を入力することで連立方程式として解くことができる電卓です。計算方法は加減法または代入法で選択でき、途中式も表示されます。
- 中学数学の問題出題ツール一覧
- 中学数学の問題をプログラムで作成して出題するツールです。問題を何度でも解く練習ができて答えもすぐに確認することができます。
- 因数分解の問題出題ツール
- 因数分解の問題を出題するツールです。条件を指定することで因数分解の問題が出題され、反復練習に役に立つツールです。
中学数学の無料問題集
