二乗に比例する関数の問題出題ツール
スポンサーリンク
二乗に比例する関数の問題解説
二乗に比例する関数の問題解説
ここでは中学数学で習う二乗に比例する関数の問題について解説していきます。
二乗に比例する関数の基本式は以下のとおりです。
二乗に比例する関数はグラフで表すと以下のようなグラフになります。
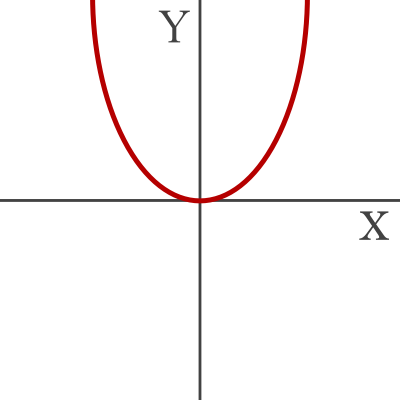
二乗に比例する関数のグラフには、「y軸に対して左右対称のグラフになる」「必ず原点を通る」「比例定数(基本式のa)が正のときは上に開き、負のときは下に開く」という特徴があります。
二乗に比例する関数の問題を解く場合には、このグラフを頭でイメージすることが非常に重要になります。細かくこの点を通るなどということは必要なく、漠然とでいいので式から上に開いているグラフか下に開いているグラフかだけでもイメージできると問題を解くときに役に立ちます。
yの値を求める
式とxの値が与えられていて、yの値を求める問題です。この問題の解き方は非常に単純で、式にxの値を代入して方程式を解く要領でyの値を求めます。
y=2x2のとき、x=3ならyの値はいくつになるか?
y = 2×32
y = 18
式の比例定数が負の数の場合、グラフで考えると下に開くグラフになるのでyの値も負の数になります。
y=-4x2のとき、x=2ならyの値はいくつになるか?
y = -4×22
y = -16
グラフを頭の中でイメージすると単純な間違いを防ぐことにもなりますので、グラフをイメージする癖をつけておきましょう。
xの値を求める
次に式とyの値が与えられていて、xの値を求める問題です。yの値を求める時と同様、式に値を代入して解きますが平方根の考え方が必要になります。つまりxの値はプラスマイナスで2つあることになります。これはグラフで考えてもわかると思いますが、y軸に対して左右対称になっているのでひとつのyに対してxの値は2つになります。
y=4x2のとき、y=16ならxの値はいくつになるか?
4x2 = 16
x2 = 4
x = ±2
問題を解くうえではあまり意識する必要はありませんが、比例定数が負の数の場合はyの値も負の数になります。これはグラフで考えれば当然ですが、比例定数が負の数の場合、下に開くのでyが正の数になることはありえません。
y=-3x2のとき、y=-75ならxの値はいくつになるか?
-3x2 = -75
x2 = 25
x = ±5
式を求める
次にxとyの値から式を求める問題です。二乗に比例する関数の式は比例定数さえわかれば式を作ることができるので、基本式にxとyの値を代入して比例定数を割り出して式を求めます。
yがx2に比例し、x=3、y=27のときの式を表せ。
27 = a×32
9a = 27
a = 3
よって式は、y = 3x2
yの値が負の場合、下に開いているグラフというのがわかりますので、比例定数も負の数になるというのがわかります。
yがx2に比例し、x=2、y=-16のときの式を表せ。
-16 = a×22
4a = -16
a = -4
よって式は、y = -4x2
変域を求める
次に変域を求める問題です。変域というのはわかりやすくいえば範囲のことで、式とxの変域からyの変域を求めます。
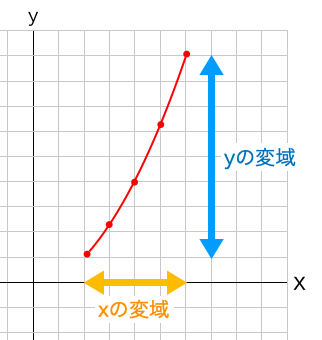
基本的な変域の求め方は、式にxの変域の最小と最大の値を代入して、yの最小と最大を割り出して変域を求めます。
y=3x2について、xの変域が2≦x≦4のときのyの変域を求めよ。
x=2のとき、y=12
x=4のとき、y=48
よってyの変域は、12≦y≦48
xの変域がマイナスの場合は、yの変域の大小に気をつけましょう。
y=4x2について、xの変域が-3≦x≦-1のときのyの変域を求めよ。
x=-3のとき、y=36
x=-1のとき、y=4
よってyの変域は、4≦y≦36
変域を求める問題でもっとも気をつけないといけないパターンがxの変域が0をまたぐときです。グラフで見ると以下のような感じになります。
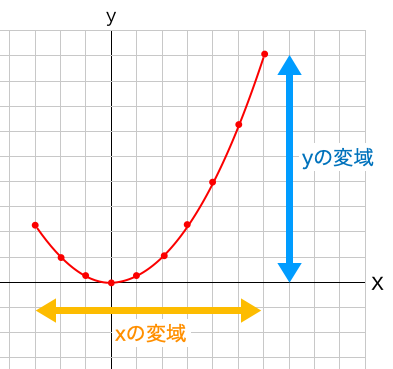
グラフで見るとわかりやすいですが、xの変域が0をまたぐと原点を通るため、yの最小が0になることがわかります。変域を求める問題はここが一番注意しなければいけません。
y=2x2について、xの変域が-2≦x≦7のときのyの変域を求めよ。
x=-2のとき、y=8
x=7のとき、y=98
よってyの変域は、0≦y≦98
また比例定数が負の場合、グラフが下に開く形になるのでxの変域が0をまたぐとyの変域の最大が0になります。
y=-4x2について、xの変域が-2≦x≦4のときのyの変域を求めよ。
x=-2のとき、y=-16
x=4のとき、y=-64
よってyの変域は、-64≦y≦0
変域を求める問題は特にグラフをイメージすることが大事になってきます。イメージするのが難しければ簡単にでもグラフを書いてみて考えると解きやすくなるかと思います。
変化の割合を求める
最後に変化の割合を求める問題です。変化の割合とは、xが変化した量に対してyが変化する量の割合がどれくらいあるかを示すものです。
一次関数の場合、グラフが直線なのでどの部分でも変化の割合は一定ですが、二乗に比例する関数ではグラフが曲線になるので変化の割合は部分によって変化します。ただ変化の割合を求める式は一次関数でも二乗に比例する関数でも同じです。
変化の割合を求める問題は大きく2つのパターンがあり、xとyの値から求める問題と式とxの値から求める問題があります。
xが1から3、yが4から36に変化するときの変化の割合を求めよ。
y=6x2について、xが1から4に変化するときの変化の割合を求めよ。
x=1のとき、y=6
x=4のとき、y=96
まとめ
二乗に比例する関数の問題を解説してきました。
二乗に比例する関数の問題は計算自体は特に複雑なこともなく難しくはありませんが、単純なミスをして点数を落としやすいことがあります。代表的なのは変域を求めるときの原点をまたぐ問題ですね。このような単純なミスを防ぐためにもしつこいようですがグラフをイメージすることが大切になってきます。グラフで考えることで単純なミスを減らすことができます。ここは是非意識して問題を解いてください。
当サイトの問題出題ツールは多くの問題パターンを解く練習ができます。グラフをイメージするトレーニングにもなりますので是非活用していただければと思います。
問題出題ツール一覧
スポンサーリンク
