一次関数の問題出題ツール

お知らせ

当サイトの問題出題ツールは問題集アプリに移行しました。今後は問題集アプリをご利用ください。

中学生向け数学の無料問題集アプリをダウンロード

一次関数の問題解説

スポンサーリンク

一次関数の問題解説

ここでは一次関数の問題について解説します。

一次関数は、yをxの一次式で表したものです。つまり、y=ax+bが一次関数の基本式になります。この基本式は一次関数の問題を解くうえで非常によく使われるので必ず覚えておきましょう。

一次関数の式をグラフで表すと以下のようなグラフになります。

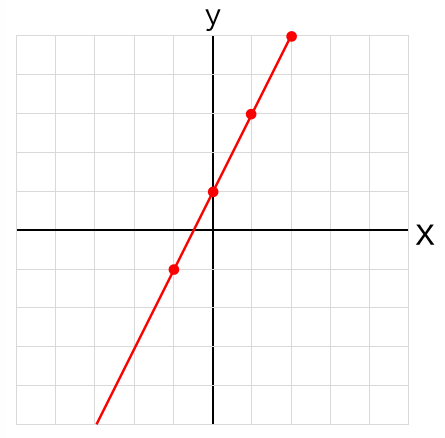
一次関数のグラフの特徴として「必ず直線になる」ということがあります。問題を解くうえでもこのグラフを頭の中でイメージするとより問題が解きやすくなります。

変化の割合・増加量を求める

まずはじめに変化の割合や増加量を求める問題です。変化の割合や増加量は以下の式によって求めることができます。

変化の割合 =
yの増加量
xの増加量

変化の割合

xが変化した量に対してyが変化する量の割合がどれくらいかを示すのが変化の割合です。一次関数においては、傾きと同じ意味となり基本式y=ax+bのaの部分です。

問題
点(6, 4)から点(9, 10)に変化したときの変化の割合を求めよ。

回答

10-4
9-6
=
6
3
= 2

xの増加量

変化の割合を求める式を使い、変化の割合とyの増加量がわかっていればxの増加量を求めることができます。

問題
変化の割合が2で、yが1から5に変化するときのxの増加量を求めよ。

回答

5-1
xの増加量
= 2

xの増加量=2

yの増加量

同じように変化の割合を求める式を使い、変化の割合とxの増加量がわかってればyの増加量を求めることができます。

問題
変化の割合が3で、xが1から3に変化するときのyの増加量を求めよ。

回答

yの増加量
3-1
= 3

yの増加量=6

傾きと切片を求める

次に一次関数の式から傾きと切片を求める問題です。

すでに説明していますが、傾きは一次関数においては変化の割合と同じ意味であり、xが変化した量に対してyが変化する量の割合がどれくらいかを示すものです。基本式y=ax+bのaの部分です。

切片はグラフにおいて、xが0のときにy軸のどこを通るかの値です。基本式y=ax+bのbが切片となります。

つまり、傾きと切片が式のどの部分かをわかっていれば特に難しい問題ではありません。

問題
一次関数y=5x+1のグラフの傾きと切片を求めよ。
回答
傾き 5, 切片 1

式を求める

与えられた条件から一次関数の式を求める問題です。一次関数の基本式はy=ax+bですので、４つの文字のうち３つがわかれば残りの１つを割り出すことができ、式を完成させることができます。

傾きと１点から

傾きとグラフ上の１点がわかっている条件で一次関数の式を求めます。つまり、基本式のa,x,yがわかっている状態なので、値を代入することでbの切片を割り出して式を完成させます。

問題
傾きが5で、点(4, 21)を通る直線の式を求めよ。
回答

y=ax+bにa=5、x=4、y=21を代入
21=5×4+b
b=1

y=ax+bにa=5、b=1を代入して式を出す
y=5x+1

切片と１点から

切片とグラフ上の１点がわかっている条件で一次関数の式を求めます。上の問題と同様に基本式にわかっている値を代入します。今回はb,x,yがわかっている状態なので、値を代入することでaの傾きを割り出して式を完成させます。

問題
切片が3で、点(4, 11)を通る直線の式を求めよ。
回答

y=ax+bにb=3、x=4、y=11を代入
11=4a+3
a=2

y=ax+bにa=2、b=3を代入して式を出す
y=2x+3

２点から

グラフ上の２点から一次関数の式を求めます。２点の座標がわかっているということはxとyの増加量がわかり、そこから変化の割合つまり傾きを算出することができます。あとは上の問題と同様に基本式に値を代入して式を導き出します。

問題
点(1, 11)と点(7, 35)を通る直線の式を求めよ。
回答

２点から傾きを求める。

a =
35-11
7-1
= 4

y=ax+bにa=4、x=1、y=11を代入
11=4×1+b
b=7

y=ax+bにa=4、b=7を代入して式を出す
y=4x+7

変域を求める

変域とはxやyの範囲のことです。例えばxの変域は「1≦x≦5」のように記述されます。これはxの範囲が1以上5以下であるという意味となります。

気をつけたいのは変域は「変化」ではなく「範囲」であるということです。例えば一次関数においてyの値が1から-3に変化することはあります。しかし「1≦y≦-3」のような変域は存在しません。変域として正しいのは「-3≦y≦1」になります。

xの変域

一次関数の式とyの変域からxの変域を求める問題です。解き方は一次関数の式にyの変域の最小と最大を代入して、xの変域の最小と最大を求めます。

問題
一次関数y=2x+6について、yの変域が8≦y≦20のときのxの変域を求めよ。
回答
1≦x≦7

yの変域

一次関数の式とxの変域からyの変域を求める問題です。上の問題と同様に式に変域の最小と最大を代入してyの変域を求めます。

問題
一次関数y=-2x-5について、xの変域が1≦x≦3のときのyの変域を求めよ。
回答
-11≦y≦-7

問題出題ツール一覧

スポンサーリンク

URLコピー